Skip to main content

OFDM系统详解

OFDM原理​

关于 OFDM 的原理，网上已经有太多的优秀文章来解释，我在这里就不再赘述了。但自己看了这么多文章，仍旧觉得理论和实际的差别还是太大，另外 OFDM 系统里许多细节也似懂非懂。

于是，我想借这篇文章来认真梳理一下 OFDM 里的一些重要概念，并且给到简洁易懂的仿真代码。

首先，我们还是来过一遍 OFDM 的定义：

Orthogonal Frequency Division Mutiplexing，全称为正交频分多址。相比于原始的 FDM，它的优势在于能够最大化频谱利用效率，不再像 FDM 那般需要留出保护带，而是不同的频谱可以彼此重叠。

关于 OFDM 的具体原理，可以参考这篇写的很好的入门博客：

给“小白”图示讲解OFDM的原理_码懂的博客-CSDN博客

了解了基础的 OFDM 原理后，我们尝试从 OFDM 系统的层面去深入理解。

OFDM 系统框图​

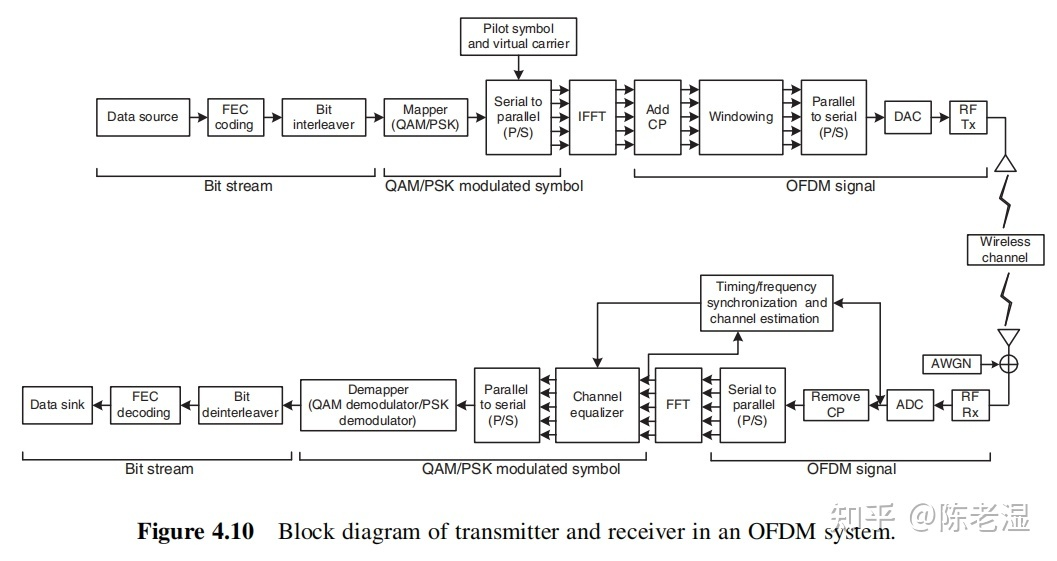
上面两张图是一个简单的 OFDM 收发机系统中英文版本，我们重点梳理其中比较重要的部分。

1. OFDM 的调制与解调​

OFDM 的输入实际上是经过 QAM/PSK 调制映射过后的符号序列，之后将符号序列转换成 N 个并行符号流（这里的 N 就是子载波个数），每 N 个经过串/并转换的符号被不同的子载波进行调制。

以前的我也认为，这里的 IFFT 和 FFT 操作是在进行信号的分析和处理，因为 IFFT 和 FFT 大家都是在 《信号与系统》这门课里学到的知识点。

于是，很多同学下意识地看到 IFFT/FFT 就把它当成是信号处理的手段，但实际上这里的 IFFT/FFT 操作只是相当于一个波形发生器。

我们这里使用 IFFT/FFT 原因是他们的公式形式和 OFDM 符号的表现形式实在是太类似了。（具体可见，这里偷个懒直接截取《MIMO-OFDM的无线通信技术及其MATLAB实现》书中的对应部分）

可能上面的公式你看着有些头大，我们再换一个角度来理解 IFFT/FFT 的作用。 下图就很好地展示了在 QAM-OFDM 情况下子载波的叠加情况。

我们一共有四个子载波频率，假如说我们把幅度和相位二值化，下图表示的信息就是（11,10,01,00） 。

而 sin + cos 的信号我们可以用欧拉公式表示成复数形式，表示为 AkA_{k}，现在我们得到的信号就变成了（A1,A2,A3,A4A_{1},A_{2},A_{3},A_{4})，然后我们再写出他们时域叠加的形式：

∑k=0n−1Akexp⁡(2πfnt)\sum_{k=0}^{n-1} A_{k}\exp(2\pi f_{n}t)

这不就是傅里叶级数的表达式嘛，自然可以用 IFFT 来进行计算了。因此，我们直接对调制后的复数信号进行 IDFT 变换（这里的 IFFT 和 IDFT 可以暂时理解成类似的变换方法，本质没有区别），得到我们想要的时域信号了。

2.保护间隔和 CP​

首先，我们来区分两个概念：子载波干扰（ICI）和符号间干扰（ISI）。

在OFDM系统，最基本的传输单位是 OFDM符号。由于同一信号的不同分量经过不同路径到达接收端的时间不一样。

如图4.14所示，如果保护间隔长度小于最大多径时延扩展，对于前一个OFDM符号的尾部已经影响到下一个OFDM符号的前端，这样就造成ISI。

当出现上面的 ISI 时，不少书籍直接引入了 CP （cyclic prefix），也就是循环前缀的概念。

其实，这里并不一定必须是 CP，只需要我们引入保护间隔的来避免 ISI 即可。其他的方法，比如说补零（ZP, Zero Padding），但这又会带来 ICI （子载波干扰）的问题。

那么什么是 ICI 呢？我们可以理解为子载波之间的正交性被破坏了。

许多书籍都直接引入了 CP 的概念来消除 ZP 带来的 ICI 的问题，但没说清楚为什么。

一个比较笼统的解释是：CP 保证了每个经历时延的子载波的连续性。假设我们添加的 CP 长度为TGT_{G}，TsubT_{sub} 表示没有保护间隔时有效的 OFDM 符号的周期。其中Tsub=1ΔfT_{sub}=\frac{1}{\Delta f}，这里的 Δf\Delta f指的是子载波的间隔。

具体的解释参考下面的博文即可，这里就不再赘述了。

OFDM专题之子载波间干扰问题（一）_李锐博恩的博客-CSDN博客

OFDM 概念辨析​

OFDM 里面涉及的小概念很多，经常学完一遍后仍然觉得云里雾里，这里借着两道例题和具体标准中的参数来进行一个汇总。

  • TuT_{u} ：有效数据部分的符号时间
  • TGT_{G}： 循环前缀的长度
  • TsT_{s}: OFDM 符号长度 Ts=Tu+TGT_{s}=T_{u}+T_{G}
  • NN： 子载波个数
  • Δf=1Tu\Delta f = \frac{1}{T_{u}} 子载波间隔
  • B=N×ΔfB = N\times\Delta f 带宽
  • Tsample=1B=TuNT_{sample}=\frac{1}{B}=\frac{T_{u}}{N} 采样时间间隔

先来看一道例题：

假设一个系统是20MHz带宽，需要留2MHz为保护带宽，剩余带宽用做数据传输。同时，假设子载波间隔为15KHz，每个子载波均采用16QAM调制，且经填充CP后，1ms能发送14个OFDM符号。请问： （1）做IFFT或者FFT的点数是多大？ （2）信息传输速率是多少？

（1）用于传输 OFDM 信号的带宽为 20-2 = 18 MHz，所以子载波个数 NN = 18MHz/15KHz = 1200，因为 IFFT 点数都是 2 的次方，所以为 2048

（2）一个符号包含 4 个bit 的信息，一个 OFDM 符号包含 1200 个子载波，所以传输速率为 4 1200 14 bits /1 ms = 67.2 Mbps。

仿真代码​

一篇很值得一读的文章，里面的仿真程序已经写的很好了，可以直接参考： OFDM完整仿真过程及解释（MATLAB） - 知乎

另外陈老师这部分关于 OFDM 的文章也值得参考，具体也有对应的代码： 《通信MATLAB仿真》合集 - 陈老湿的文章 - 知乎 https://zhuanlan.zhihu.com/p/385096476

值得细读的文章​

1.OFDM 简洁的矩阵表示： 第7章：OFDM的矩阵表示 - 知乎

2.两道 OFDM 的计算题 第7章：OFDM两道计算题 - 知乎

Reference​

无线通信基础2：深入理解OFDM（含Matlab代码） - 知乎 第7章：OFDM 信道估计与均衡（5） - 知乎 OFDM完整仿真过程及解释（MATLAB） - 知乎